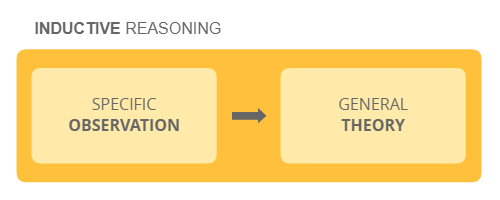
What is Inductive Reasoning: The Key to Logical Thinking

Inductive reasoning is a fundamental cognitive process that plays a crucial role in our everyday lives and the scientific community. It draws general conclusions or makes predictions based on specific observations or evidence. Unlike deductive reasoning, which moves from general principles to specific instances, inductive reasoning moves in the opposite direction, from specific observations to broader generalizations.

This article provides a comprehensive understanding of inductive reasoning, its principles, and its applications across various domains.

What is Inductive Reasoning?

Inductive reasoning is a type of logical reasoning that forms general conclusions based on specific observations or evidence. It is a bottom-up approach where specific instances or examples are analyzed to derive broader generalizations or theories. In inductive reasoning, the conclusions are probabilistic rather than specific, as they are based on patterns and trends observed in the available evidence.

The strength of the conclusions in inductive reasoning depends on the quality and quantity of the evidence, as well as the logical coherence of the reasoning process. Inductive reasoning is commonly used in scientific research and everyday life to make predictions, formulate hypotheses, and generate new knowledge or theories. It allows for the exploration and discovery of new ideas by building upon observed patterns and relationships in the data.

Types of Inductive Reasoning

The types of inductive reasoning provide valuable tools for making generalizations, predictions, and drawing conclusions based on observed evidence and patterns. Different types are commonly used to make inferences and predictions. Below are the main types:

Inductive Generalization

Inductive generalization refers to the process of inferring a general rule or principle based on specific instances or examples. It makes a generalized statement or conclusion about a whole population or category based on a limited sample or set of observations. Inductive generalization aims to extend the findings from specific cases to a broader context, providing a basis for making predictions or forming hypotheses.

Statistical Induction

Statistical induction, also known as statistical reasoning, is a method that draws conclusions about a population based on a statistical analysis of a sample. It has the principles of probability and statistical inference to make inferences and predictions about the larger population from which the sample was drawn. By analyzing the data collected from the sample, statistical induction allows researchers to estimate population parameters, test hypotheses, and make probabilistic statements about the likelihood of certain events or outcomes occurring.

Causal Reasoning

Causal reasoning seeks to understand the cause-and-effect relationships between variables or events. It identifies and analyzes the factors that contribute to a particular outcome or phenomenon. This type of reasoning establishes a cause-effect relationship by observing patterns, conducting experiments, or using statistical methods to determine the strength and direction of the relationship between variables. It helps researchers understand the underlying mechanisms behind an observed phenomenon and make predictions about how changes in one variable may affect another.

Sign Reasoning

Sign reasoning, also known as semiotic reasoning, makes interpretation and analyzes signs, symbols, or indicators to draw conclusions or make predictions. It understands that certain signs or signals can signify or indicate the presence of a specific phenomenon or event. It observes and interprets patterns, relationships, or correlations between signs and the phenomena they represent. This allows researchers to uncover hidden meanings, infer intentions, and gain insights into human communication and expression.

Analogical Reasoning

Analogical reasoning is a cognitive process that draws conclusions or makes inferences based on the similarities between different situations, objects, or concepts. It operates on the idea that if two or more things share similar attributes or relationships, they are likely to have similar properties or outcomes. Analogical reasoning allows individuals to transfer knowledge or understanding from a familiar or known domain to an unfamiliar or unknown domain. By recognizing similarities and making comparisons, analogical reasoning enables individuals to solve problems, make predictions, generate creative ideas, and gain insights.

Examples of Inductive Reasoning

These examples illustrate how inductive reasoning can be applied in various contexts to draw conclusions, make predictions, and gain insights based on observed evidence and patterns:

Inductive Generalization

If you observe that several cats you encounter are friendly and approachable, you may generalize that most cats are friendly. Another example is, if we observe that a few students in a class are diligent and hardworking, we may generalize that the entire class possesses these characteristics.

Statistical Induction

Based on survey data, if it is found that a majority of customers prefer a particular brand of smartphones, it can be statistically inferred that the brand is popular among the wider population. Or for instance, if a survey finds that a majority of respondents prefer a certain brand of coffee, we can statistically infer that the preference holds true for the broader population.

Causal Reasoning

When studying the effects of exercise on weight loss, if you consistently find that participants who engage in regular exercise tend to lose more weight, you can infer that there is a causal relationship between exercise and weight loss. Another example, if studies consistently show a correlation between smoking and lung cancer, we can infer a causal link between the two.

Sign Reasoning

If you notice dark clouds, strong winds, and distant thunder, you may infer that a storm is approaching. Or another example, doctors use various signs, such as fever, cough, and sore throat, to diagnose a common cold.

Analogical Reasoning

If you discover that a new medication is effective in treating a certain type of cancer, you may infer that a similar medication could be effective in treating a related type of cancer.

Pros and Cons of Inductive Reasoning

What is inductive reasoning? Inductive reasoning refers to the cognitive process of drawing general conclusions based on specific observations or evidence. It is a valuable tool for making generalizations and predictions in various fields of study. But, like any reasoning method, inductive reasoning has its own set of pros and cons that are important to consider.

Exploring the advantages and limitations of inductive reasoning allows us to harness its strengths while being mindful of its potential shortcomings. Below are the pros and cons of Inductive Reasoning.

Pros of Inductive Reasoning

Flexibility: It allows for flexibility and adaptability in drawing conclusions based on observed patterns and evidence, making it suitable for exploring new or unfamiliar areas of knowledge.

Creative Problem Solving: It encourages creative thinking and the exploration of new possibilities by identifying patterns, connections, and relationships.

Hypothesis Generation: It can generate hypotheses or theories that can be further tested and refined through empirical research, leading to scientific advancements.

Real-World Application: It is often used in fields such as social sciences, market research, and data analysis, where generalizations and predictions based on observed patterns are valuable.

Cons of Inductive Reasoning

Potential for Error: It is susceptible to errors and biases, as conclusions are based on limited observations and may not account for all relevant factors or variables.

Lack of Certainty: It does not guarantee absolute certainty or proof. Conclusions drawn through induction are based on probabilities rather than definitive truths.

Sample Size and Representativeness: The reliability and generalizability of inductive reasoning depend on the sample size and representativeness of the observed data. A small or unrepresentative sample can lead to inaccurate conclusions.

Potential for Overgeneralization: Inductive reasoning can sometimes lead to overgeneralization, where conclusions are applied to a broader population without sufficient evidence, leading to inaccurate assumptions.

The Problem of Induction

The problem of induction is a philosophical challenge that questions the justification and reliability of inductive reasoning. It was famously addressed by the Scottish philosopher David Hume in the 18th century. The problem arises from the observation that inductive reasoning relies on making generalizations or predictions based on past observations or experiences. However, the problem of induction highlights that there is no logical or deductive guarantee that future events or observations will conform to past patterns.

This problem challenges the assumption that the future will resemble the past, which is a fundamental basis of inductive reasoning. But even if we observe a consistent pattern in the past, we cannot be certain that the same pattern will continue in the future. For example, if we observe the sun rising every day for thousands of years, it does not logically guarantee that it will rise tomorrow. The problem lies in the gap between observed instances and the generalization or prediction made based on those instances.

This philosophical challenge poses a significant hurdle for inductive reasoning because it undermines the logical foundation of drawing reliable conclusions based on past observations. It raises questions about the reliability, universality, and certainty of inductive reasoning. However, the problem of induction serves as a reminder to approach inductive reasoning with caution and to be aware of its limitations and potential biases. It highlights the need for critical thinking, rigorous testing, and the continual reassessment of conclusions to account for new evidence and observations.

Bayesian Inference

Bayesian inference is a statistical approach to reasoning and decision-making that updates beliefs or probabilities based on new evidence or data. It is named after Thomas Bayes, an 18th-century mathematician and theologian who developed the foundational principles of Bayesian inference.

At its core, Bayesian inference combines prior beliefs or prior probabilities with observed data to generate posterior beliefs or probabilities. The process begins with an initial belief or prior probability distribution, which represents our subjective knowledge or assumptions about the likelihood of different outcomes. As new evidence or data becomes available, Bayesian inference updates the prior distribution to yield a posterior distribution that incorporates both the prior beliefs and the observed data.

The theorem quantifies how the observed data supports or modifies our initial beliefs. By explicitly incorporating prior probabilities, it allows for a more nuanced and subjective approach to reasoning. It also facilitates the integration of new data as it becomes available, allowing for iterative updates and revisions of beliefs.

Inductive Inference

In inductive inference, we move from particular observations or examples to broader generalizations or hypotheses. Unlike deductive reasoning, which is based on logical deductions from premises to reach certain conclusions, inductive inference makes probabilistic judgments and draws probable conclusions based on the available evidence.

The process of inductive inference typically involves several steps. First, we observe or gather data from specific cases or instances. These observations could be qualitative or quantitative, and they provide the basis for generating hypotheses or generalizations. Next, we analyze the collected data, looking for patterns, trends, or regularities that emerge across the observations. These patterns serve as the basis for formulating generalized statements or hypotheses.

One common form of inductive inference is inductive generalization, where we generalize from specific instances to broader categories or populations. For example, if we observe that all the swans we have seen are white, we may generalize that all swans are white. However, it is important to note that inductive generalizations are not infallible and are subject to exceptions or counterexamples.

Another type of inductive inference is analogical reasoning, where we draw conclusions or make predictions based on similarities between different situations or domains. By identifying similarities between a known situation and a new situation, we can infer that what is true or applicable in the known situation is likely to be true or applicable in the new situation.

Ready-To-Go Templates In All Popular Sizes

Mind the Graph platform is a valuable tool that assists scientists in creating visually compelling and scientifically accurate graphics. With its ready-to-go templates available in all popular sizes, the platform streamlines the process of generating high-quality visuals.

Whether scientists need to create informative scientific posters, engaging presentations, or illustrative figures for research articles. The platform’s templates cater to various scientific disciplines, ensuring that scientists can present their work in a visually appealing and professional manner. Mind the Graph empowers scientists to effectively convey complex information through visually captivating graphics, enabling them to enhance the impact and reach of their research.